أي الأعداد التالية مربع كامل

أي الأعداد التالية مربع كامل؟ يأتينا هذا السؤال من منهج مادة الرياضيات، وهو سؤال شائع في كافة الفئات السنية والمراحل الدراسية، فما هو عدد المربع الكامل، وكيف يمكننا معرفته؟ سنعرفكم إلى كافة المعلومات الخاصة بالأعداد المربعة، وسنجيبكم عن سؤال أي الأعداد التالية مربع كامل عبر موقع البلد.

أي الأعداد التالية مربع كامل؟

في علم الرياضيات يُقال على العدد أنه مربع كامل (Square number) في حال ما كان العدد طبيعي ومساوٍ لمربع عدد صحيح ما، قد يكون هذا العدد الصحيح موجب، أو سالب، وحتى صفري، ويمكننا أيضًا القول إنه عدد يساوي حاصل ضرب عدد ما آخر في نفسه.

بتطبيق هذه الشروط يمكنك بسهولة الإجابة على سؤال أي الأعداد التالية مربع كامل، فما معنى هذه الشروط؟ الشرح التفصيلي لهذه الشروط يتمثل فيما يلي:

• كون العدد طبيعي يعني أنه عدد صحيح موجب، وهي الأعداد مثل 1 و2 و3 حتى ما لا نهاية ، والعلماء يضيفون الرقم 0 إلى هذه المجموعة أيضًا.
• أن يكون العدد مساوٍ لمربع عدد آخر صحيح يعني أنه في حال ما ربعت رقم معين، ستجد أن حاصل تربيعه سيكون هو العدد المربع الصحيح.
• يعتبر هذا الشرط صورة من الشرط أعلاه، فحاصل ضرب العدد في نفسه هو مربع العدد، وحتى يكون العدد مربع كامل عليه أن يكون مساويًا لحاصل ضرب عدد آخر في نفسه وهو ما يشكل مربعه.

في حال ما لم يكن لهذا العدد الإمكانية على الانقسام إلى عددين مضروبين في نفسهم بشكل مربع كامل، فإن هذا العدد يعد خالٍ من المربعات، فلا يعتبر من بين الأعداد التي تمثل مربع كامل.

قد يبدو الكلام أعلاه معقدًا بعض الشيء، لكن ثق بي الأمر أبسط من ذلك بكثير عزيزي القارئ، وسيكون واضحًا بشكلٍ أكبر فيما يلي من سطور وفقرات عند إعطاء الأمثلة التي تعزز الشرح فيما يخص الأعداد المركبة.

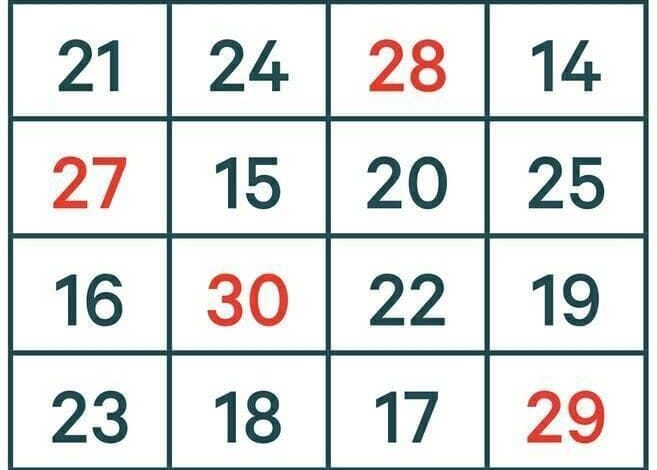
بعد أن تعرفنا بشكل سطحي مبسط على الأعداد التي تُمثل وتشكل المربع الكامل، سنتطرق وإياكم إلى الحديث عن إجابة سؤال أي الأعداد التالية مربع كامل، فهذا السؤال جاء في منهج الرياضيات بين الأسئلة الخاصة بدرس المربع الكامل، وكانت صيغة السؤال كالتالي: (أي الأعداد التالية مربع كامل)، وكان السؤال مرفقًا بالصورة أدناه.

الإجابة على السؤال المذكور أعلاه أي الأعداد التالية مربع كامل، تعد (1، 4، 9، 16، 25، 36، 49، 64، 81)، وفيما يلي سنعطيكم أمثلة أكثر على الأعداد التي تُشكل مُربع كامل، كما أننا سنوضح سبب كون إجابة السؤال السابق أي الأعداد التالية تُمثل مربع كامل هي الأرقام التسعة التي تم ذكرها أعلاه.

كيفية معرفة العدد الذي يمثل المربع الكامل

بعد أن قُمنا وإياكم بالتعرف إلى إجابة سؤال أي الأعداد التالية مربع كامل، سنوضح لكم لما تمثل هذه الأعداد بالذات مربعات كاملة، في واقع الأمر تعتبر الصيغة الرياضية للتعبير عن المربع الكامل متمثلة في  أو  ، والرقم  هنا يمثل عدد صحيح.

كما كنا قد ذكرنا أعلاه أن العدد الصحيح هو عدد موجب، أو سالب، وحتى الصفر تُشكل عدد صحيح، فكل الأعداد صحيحة عدا الكسرية.

بشكل أوضح نتناول الأرقام التي أجابت عن سؤال أي الأعداد التالية مربع كامل، وهي كل من (1، 4، 9، 16، 25، 36، 49، 64، 81)، فبالحديث عن كل رقم نجد أن هذه الأرقام طبيعية، وهو الشرط الأول، أي أنها موجبة وغير كسرية، وهذا الشرط الأول فيما يخص الأعداد المربعة.
أما الشرط الثاني الواجب تحقيقه هو أن تكون هذه الأرقام التي تُشكل مربع كامل، تساوي حاصل ضرب عدد صحيح في نفسه، أو مربع هذا العدد، فهل تستوفي هذه الأعداد هذا الشرط؟ دعونا نرى ذلك فيما يلي.

العدد الأول الذي يعبر عن الإجابة على سؤال أي الأعداد التالية مربع كامل هو العدد 1، والعدد 1 يمثل حاصل ضرب 1×1 ويُمثل أيضًا مربع العدد 1 وهو  إذًا فهذا العدد يمثل مربع كامل.

عليك أن تأخذ في عين الاعتبار أن المربع الكامل هو مربع عدد صحيح الموجبة أو السالبة وحتى الصفرية، ما يعني أن العدد 1 عدد مربع كامل للعدد  فهو مربع  وحاصل ضرب  أيضًا.

يمكنك فهم أعداد المربع الكامل من هذه الصورة بشكل أكبر، فيمكنك أن ترى أن كل رقم هنا ينغلق ليشكل شكل المربع، فأضلاعه جميعها متساوية، فتجد أن رقم واحد يُمثله مربع واحد وجميع أضلاعه متساوية، والرقم 25 يمثله 25 مربع، وتجد أن كل ضلع له يتكون من 5 مربعات، إذا فهو مربع كامل للعدد 5 والعدد  أيضًا.

كما أن الرقم 49 يعتبر مربع كامل لأنه يحتوي على 49 مربع، وسنجد أن كافة أضلاه هذا المربع الأربعة تتكون من 7 مربعات، فنستنتج أن العدد 49 هو المربع الكامل للعدد 7 والعدد.

أمثلة على الأعداد التي تعبر عن مربع كامل

الأعداد التي تُمثل مربع كامل لا حصر لا، فبشكل عام هي أعداد يعبر الجذر التربيعي الخاص بها عن عدد طبيعي وهو عدد موجب حصرًا ولا كسور فيه، ومن أمثلة هذه الأعداد التي تعبر عن مربع كامل كل مما يلي:

1 يمثل مربع كامل للعدد 1 و1- فهو يمثل حاصل ضربه في نفسه.

4 يمثل مربع كامل للعدد 2 و2- فهو يمثل تربيعه وحاصل ضربه في نفسه.

9 يمثل مربع كامل للعدد 3 و-3 فحاصل ضرب 3  في ذاته أو مربع 3  هو 9

16  4 و4-

25  5 و5-

36  6 و6-

49  7 و7-

64  8 و8-

81  9 و9-

100  10 و10-

كما يمثل العدد 0 المربع الكامل للعدد 0 فقط، فالصفر ليس له سالب.

والأرقام التي تعبر عن المربع الكامل لا نهاية ولا حصر لها، فالقائمة تطول من 0 وحتى مالا نهاية، فأي رقم طبيعي أي أنه صحيح وموجب بين 0 وحتى  يعتبر عدد مربع كامل في حال ما كان له جذر تربيعي يمثله عدد صحيح مثل 1، 2، 3، …… إلخ.

تطبيق عملي لتسهيل فهم المربع الكامل

يمكن شرح المربع الكامل لطفل صغير بشكل عملي سهل عن طريق استخدام العملات المعدنية، فالعملات المعدنية التي يتم رصها بجوار بعضها لتكوين مربع غير مفرغ تعبر عن عدد يمثل مربع كامل، من الأمثلة على هذا التطبيق ما يلي:

• تمثيل العدد 4 كمربع كامل باستخدام العملات المعدنية

نجد هنا أن هذا الشكل عبارة عن 4 عملات معدنية ممثلة للمربع الكامل 4، وبما أن كل ضلع منها يتكون من عملتين، إذا فالرقم 4 هو المربع الكامل للعدد 2، ولا ننسى السالب منه بكل تأكيد.

• تمثيل العدد 9 كمربع كامل باستخدام العملات المعدنية

يمثل العدد 9 مربع كامل للعدد 3 الذي يشكل عدد العملات المكونة لأضلاعه.

• تمثيل العدد 16 كمربع كامل باستخدام العملات المعدنية

نجد أن العدد 16 هو المربع الكامل للعدد 4، وهو العدد الذي يكون عدد العملات فيه أضلاع المربع.

• العدد المربع الكامل يمكن تمثيله باستخدام العملات المعدنية عن طريق إعداد مربع يساوي عدد العملات المعدنية في أي عمود فيه عدد العملات المعدنية في أي صف، وليس الأضلاع فقط، فتمثيل الرقم 12 مثلًا ممكن من خلال الشكل التالي، ولكن كما نرى فالمربع فارغ من المنتصف، لذا لا يعتبر الرقم 12 مربع كامل، كما أن الجذر التربيعي له لا يمثل عدد صحيح فهو 3.4، على عكس 144 فجذره التربيعي 12.

بعد أن تعرفنا سويًا إلى إجابة أي الأعداد التالية مربع كامل، بالإضافة إلى كيفية معرفة المربع الكامل وشروطه، هل يمكنكم معرفة ما إن كان الرقم 361 يمثل مربع كامل أم لا؟