قانون حساب الوتر في مثلث قائم الزاوية
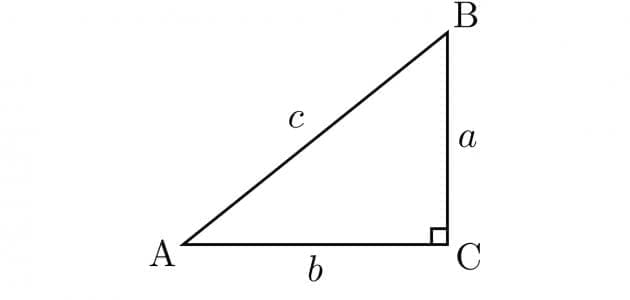
قانون حساب الوتر في مثلث قائم الزاوية من القوانين الهامة في الرياضيات، فالمثلث القائم نوع من أنواع المثلثات، يحتوي على زاوية قائمة قياسها 90 درجة والضلع المقابل لهذه الزاوية يطلق عليه اسم الوتر، أما الضلعان الآخران فيطلق عليهما اسم ساقي المثلث قائم الزاوية، فدعونا نتعرف سوياً من خلال هذا المقال على هذا القانون وبعض الأمثلة التوضيحية عبر موقع البلد
قانون حساب الوتر في مثلث قائم الزاوية
تعد نظرية فيثاغورث واحدة من أهم النظريات التي نتجت عن العديد من الدراسات التي أجريت حول المثلثات، وقد سميت بهذا الاسم نسبة إلى عالم الرياضيات المشهور فيثاغورث، كما أنه كان فيلسوف وعالم فلك في اليونان القديمة.
وقد نصت هذه النظرية على أن الجذر التربيعي للوتر في المثلث قائم الزاوية يساوي مجموع مربعي الضلعين الآخرين، ويمكن كتابة النظرية كمعادلة تربط بين أطوال المثلث ويعبر عنها بهذا القانون:-
(طول الوتر)²= (طول الضلع الأول)²+( طول الضلع الثاني)²
أمثلة تطبيقية على قانون الوتر
يوجد العديد من الأمثلة التي يمكن الاستعانة بها لفهم قانون الوتر في المثلث ذو الزاوية القائمة، ومن ضمن هذه الأمثلة الآتي:
1- المثال الأول
إذا كان المثلث الذي أضلاعه (أ ، ب) والوتر (ج) مثلث قائم الزاوية في ب وطول ضلع ب ج يساوي 12 سم وطول الضلع أ ب يساوي 5 سم، أوجد طول الضلع أ ج.
الحل
إن المثلث قائم الزاوية عند ب لذلك فإن الضلع المقابل للزاوية ب هو أ ج وهو الوتر، ولإيجاد طول هذا الضلع لابد من اتباع الخطوات الآتية:-
(طول الوتر)²= (طول الضلع الأول)²+( طول الضلع الثاني)²
(5) ² + (12) ² = 25 + 144 = 169، وبأخذ الجذر التربيعي للطرفين فإن طول الوتر سيكون 13 سم.
2- المثال الثاني
مثلث زاويته قائمة فيه طول الضلع الأول يساوي 9 سم وطول الوتر يساوي 15 سم، أوجد طول الضلع المجهول.
الحل
(طول الوتر) ² = (طول الضلع الأول) ² + (طول الضلع الثاني) ²
(15) ² = (9) ² + (طول الضلع الثاني) ²
225 = 81 + (طول الضلع الثاني) ²
وبأخذ الجذر التربيعي للطرفين، فإن طول الضلع الثاني سيكون 12 سم.
من هنا نكون قد توصلنا إلى ختام موضوعنا بعد أن استعرضنا قانون حساب الوتر في مثلث قائم الزاوية ونتمنى أن يكون المقال حاز على إعجابكم حرصاً منا على رضاكم ونيل ثقتكم، وفي النهاية نوصيكم بمشاركته على وسائل التواصل الاجتماعي حتى تعم الفائدة على أكبر عدد من الأشخاص.





