مساحة المثلث متساوي الأضلاع

elneelمنذ 4 أسابيع

0 7 10 دقائق

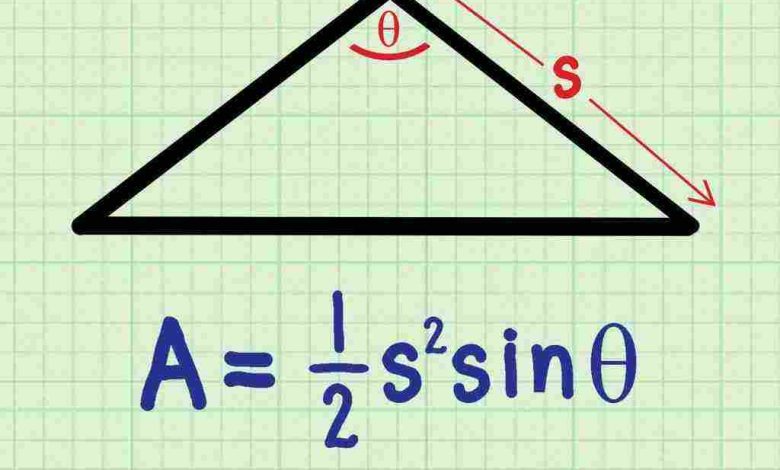
مساحة المثلث متساوي الأضلاع علم الهندسة من أهم العلوم الموجودة لأنها تستخدم في حل الكثير من المشاكل وقد تم اكتشاف هذا العلم من قبل المهندسون ويوجد الكثير من الأشكال الهندسية مثل المثلث بجميع أنواعه وسنتعرف على مساحة المثلث متساوي الأضلاع، لذا تابعوا معنا السطور التالية عبر موقع البلد .

معلومات عن علم الهندسة

يصنف علم الهندسة أنه من أهم وأبرز العلوم الموجودة حالياً لأنه يتضمن الكثير من العلوم والنظريات والتطبيقات والرياضيات والقواعد التي تستخدم في حل جميع المشاكل المختلفة.
حدثت كل هذه القواعد والنظريات وغيرها من خلال اكتشاف المهندسين لكيفية عمل الأشياء.
ليس ذلك فقط فتم اكتشاف مجموعة تتكون من جميع الاستخدامات العلمية التي تساعد في اكتشاف وتحقيق جميع الاكتشافات العلمية.
في الوقت الحالي يقوم كل من المهندسين والعلماء والمخترعين في اختراع الكثير من الابتكارات التي تساعد في تطور الحالات البشرية بشكل عام.
ولكن كل الفضل الناتج من هذه الاختراعات والابتكارات يعود في النهاية إلى المهندسين لأنهم يحققون دوراً دور فعال جداً في إظهار كل هذه الابتكارات إلى العالم الخارجي.
أما بالنسبة لتاريخ الهندسة فهو يعتبر جزء لا يتجزأ من تاريخ وجود الحضارة الإنسانية التي تشمل جميع الوظائف الهندسية التي ينفذها المهندسين في المجالات المختلفة مثل التطوير والتصميم والتعديل.
وبعض المجالات والأنظمة الأخرى الأكثر أهمية مثل التقييم والاختبار والفحص والتركيب والصيانة التي تتم على الأنظمة المختلفة والمتنوعة.
بالإضافة إلى كل هذا يتم أيضاً تحديد جميع العمليات والمواد ويتم أيضاً الإشراف ومراقبة البناء والتصنيع والخدمات الاستشارية.
تعتبر تقديم الخدمات الاستشارية من أهم الوظائف والخدمات والمسئوليات التي تقدم في مجالات الهندسة.

المثلثات

المثلثات تعد واحدة من أهم الأشكال الهندسية التي توجد في علم الهندسة ولها استخدامات كثير جداً.
أما بالنسبة للمثلث فهو عبارة عن مثلث ثلاثي الحواف ويتكون من ثلاثة رؤوس هندسية وكما ذكرت الهندسة الإقليدية أن مجموع قياسات زوايا المثلث الداخلية في الفضاء الإقليدي تكون دائماً 180 درجة قياسية.
من خلال هذه القياسات يتم تحديد قياس الزاوية الثالثة ل أي مثلث مهما كان نوعه بالنظر إلى الزاويتان الظاهرتان.
في أي مثلث توجد زاوية تسمي بالزاوية الخارجة للمثلث وتعرف بأنها الزاوية التي تمثل زوج خطي يكون مكمل للزاوية الداخلية للمثلث.
بالإضافة إلى ذلك فإن المقياس الخاص بالزوايا الخارجية للمثلث يساوي مجموع قياس الزاويتان الداخليتان الغير مجاورتين لها.
وهذه تعتبر النظرية الخاصة بالزاوية الخارجة مجموع قياسات الزوايا الخارجية لأي مثلث مهما كان نوعه تساوي 360 درجة.
المثلثات لها أنواع كثيرة جداً ولكنها تختلف من حيث الخصائص والتفاصيل التي يتضمنها كل مثلث.

تكوين المثلث

يتكون المثلث من ثلاثة قطع مستقيمة الشكل وتسمي هذه القطع بالأضلاع.
في نهاية هذه القطع المستقيمة توجد نقطة وهي نقطة تلاقي الأضلاع مع بعضها البعض وتسمى هذه النقاط الرؤوس أو الزوايا.
وبالتالي فأن المثلث يمتلك ثلاث زوريا أو ثلاث رؤوس مجموع قياسات هذه الزوايا تكون 180 درجة.
أصغر ضلع في هذا المثلث يقابل دائماً أصغر زاوية من الزوايا الداخلية للمثلث.
ويمكن تعريف رأس المثلث أنها هي زاوية المثلث ويمتلك كل مثلث ثلاث رؤوس.
أما القاعدة هي الضلع المرسوم الذي يكون غير متساوي مع باقي أضلاع المثلث وهذه القاعدة تستخدم في حساب مساحة المثلث.
متوسط المثلث وهو الخط الممتد بين رأس المثلث حتى منتصف الضلع المقابل له وكل مثلث يمتلك ثلاثة منها وتتقاطع كل هذه الأضلاع في نقطة واحدة تسمى بالنقطة المركزية للمثلث.
الارتفاع ويعرف بأنه العمود الذي يمتد من رأس المثلث وحتى القاعدة المقابلة له وبما أن هناك المثلث يمتلك ثلاث زوايا فأذن يمتلك ثلاث ارتفاعات أيضاً وهي ناتج تقاطعات ملتقى الارتفاعات مع بعضها.

أنواع المثلثات حسب أطوال الأضلاع

النوع الأول هو المثلث متساوي الأضلاع وهو عبارة عن مثلث جميع أضلاعه الثلاثة تكون متساوية في الطول.
جميع الزوايا الخاصة به تكون متساوية أيضاً ويكون قياس كل زاوية منهما 60 درجة.
النوع الثاني هو المثلث متساوي الساقين وهو عبارة عن مثلث له ضلعان متساويان في الطول ويمتلك زاويتان متساويتان في القياس وهاتان الزاويتان هما زاويتان القاعدة.
النوع الثالث هو مثلث مختلف الأضلاع وهو مثلث لا يملك أي أضلاع متساوية في الطول ولا يمتلك أي زوايا متساوية في القياس أيضاً.

أنواع المثلثات حسب الزوايا

النوع الأول هو مثلث حاد الزوايا ويعرف بأنه مثلث تكون كل زواياه أقل من 90 درجة.
المثلث منفرج الزاوية ويعرف بأنه المثلث الذي يمتلك زاوية قياسها أكبر من 90 درجة وتسمى بـ الزوايا المنفرجة.
المثلث قائم الزاوية ويعرف بأنه مثلث يتكون من ثلاث زوايا قائمة تكون قياس كل زاوية 90 درجة ويمتلك هذا النوع من المثلثات عدة أنواع مختلفة.

أنواع المثلث القائم الزاوية

المثلث القائم هو المثلث الذي يمتلك ثلاث زوايا قوائم تكن قياس كل زاوية منهما 90 درجة ويمتلك المثلث القائم مجموعة من الأنواع وتسمي أنواع قائمة الزوايا الخاصة وتكون كما يلي.
النوع الأول هو مثلث 90-45-45 وهو مثلث قائم الزاوية وتكون كل زاوية من زواياه 45 درجة.
بالإضافة إلى أنه مثلث متساوي الساقين وأضلاع هذا المثلث تكون في حالة تناسب دائماً ويكون هذا التناسب بنسبة 1: 3√: 2 وهذه النسبة ثابتة في جميع المثلثات القائمة.
النوع الثاني 90-45-45 هو مثلث قائم الزاوية ويكون قياس زاوية واحدة من زواياه 60 درجة والزاوية الأخرى تكون قياسها 30 درجة والزاوية الثالثة تكون ناتج جمعهم وطرح الناتج من 180 درجة.
في هذا المثلث تكون أضلاع هذا المثلث في حالة توازن مع بعضها البعض ويكون هذا التناسب بنسبة 1: 3√: 2 وهذه النسبة ثابتة.

خصائص المثلث العامة

مجموع قياسات زوايا المثلث تساوي 180 درجة.
مجموع أي ضلعين في المثلث تكون أكبر من طول الضلع الثالث.
الفرق بين طول أي ضلعين من أضلاع المثلث تكون أقل من طول الضلع الثالث.
الزاوية الخارجية لأي مثلث يساوي حاصل جمع الزاويتان الداخليتان البعيدتان وهذه الخاصية مشهورة جداً وتسمى أنها خاصية الزاوية الخارجة وتكون موجودة في جميع أنواع المثلثات.
الضلع المقابل للزاوية الأكبر في المثلث يكون هو الضلع الأكبر.
إذا كانت الزوايا المتقابلة في المثلثان فينتج عن ذلك تساوي الأضلاع أيضاً وهذا في جميع أنواع المثلثات.
مساحة أي مثلث تساوي 0.5 طول القاعدة * الارتفاع.
محيط أي مثلث يساوي مجموع جميع الأضلاع الثلاثة للمثلث.
المثلث الذي يحتوي على زاوية واحدة أكبر من 90 درجة يسمي مثلث منفرج الزاوية Obtuse angle triangle.
المثلث الذي يكون مجموع جميع زواياه أقل من 90 درجة يكون مثلث حاد الزاوية ويعرف بالانجليزية أنه Acute angle triangle.

خصائص متوسط المثلث

يقوم بتنصيف زوايا الرأس التي تكون موجودة ما بت ضلعين متساويين في المثلثات المتساوية الساقين وفي المثلث المتساوي الأضلاع أيضاً.
في أي مثلث يوجد ثلاث خطوط متوسطة تتقاطع هذه الخطوط في نقطة واحدة تسمي هذه النقطة المركزية أو كما يقال عليها باللغة الإنجليزية Centroid.
يتم تقسيم كل من هذه الخطوط النسبة ثابتة دائماً في جميع المثلثات 2:1.
يمكن تصنيف كل متوسط من متوسطات المثلثات إلى مثلثين منفصلين ولكن ذات مساحة واحدة.
من خلال نظرية أبولونيوس يمكن حساب طول متوسط المثلث كما يلي.
م أ= ((2بَ²+ 2جَ²- أَ²) ÷4) √.
أو م ب= ((2أَ²+ 2جَ²- بَ²) ÷4) √.
أو م ج= ((2بَ²+ 2أَ²-جَ²) ÷4) √.
ويمكن معرفة كل رمز من رموز هذا القانون عن طريق فهم وقراءة ما يلي.
م ج طول خط المتوسط النازل من الرأس ج، جَ: طول الضلع المقابل للرأس ج.
م ب طول خط المتوسط النازل من الرأس ب، بَ: طول الضلع المقابل للرأس ب.
م أ طول خط المتوسط النازل من الرأس أ، أَ: طول الضلع المقابل للرأس أ.

خصائص ارتفاع المثلث

ارتفاع المثلث من الممكن أو يقع خارج المثلث أو يقع داخل المثلث.
كل مثلث يمتلك ثلاث ارتفاعات محتملة ويكون كل واحد من هذه الارتفاعات ممتد من رأس من رؤوس المثلث.
الارتفاع الذي يكون من الرأس ويصل إلى الضلع المقابل له في المثلث يعتبر أقصر ارتفاع.
جميع الارتفاعات الثلاثة تلتقي دائماً في نقطة واحدة وذلك بعيداً عن شكل المثلث ونوعه وتسمى نقطة التلاقي ملتقى الارتفاعات الثلاثة وتسمى في اللغة الإنجليزية Ortho-centre of the triangle.

خصائص المثلث متساوي الأضلاع

جميع الزوايا الداخلية للمثلث المتساوي الأضلاع تكون متساوية.
كل زاوية من زواياه تكون 60 درجة.
يكون كل من المنصف العمودي وخط الخاص بالمستوى ومنصف الزوايا لكل ضلع من الأضلاع هو نفس الخط.
ويكون الطول متساوي بالنسبة لجميع الأضلاع ويساوي (3√×س) ÷2.
هنالك رمز واحد في هذا القانون وهو حرف ال س ويقصد به طول ضلع للمثلث المتساوي الأضلاع ومن هذه النقطة يمكن القول إن أطوال خطوط متوسطات المثلث الثلاثة في المثلث المتساوي الأضلاع تكون دائماً متساوية.

نظريات المثلث قائم الزاوية

المثلث القائم هو المثلث الذي يحتوي على زاوية تكون قياسها 90 درجة ويعرف هذا المثلث بالإنجليزية أنه Right-angle triangle.
أما بالنسبة لباقي الزوايا الخاصة بهذا المثلث فتكون عبارة عن زوايا حادة والضلع الذي يقابل الزاوية القائمة يسمي في الهندسة الوتر ويطلق عليه في اللغة الإنجليزية Hypotenuse.
ويعتبر هذا الضلع أطول ضلع في المثلث القائم الزاوية ويمكن حساب طول هذا الضلع بمجموعة مختلفة من الطرق والنظريات ولكن من أهمها النظرية المعروفة وهي نظرية فيثاغورس.
نظرية فيثاغورس تقول إن مجموع مربع كل ضلع من أضلاع المثلث القائم الزاوية يساوي مربع طول الوتر ويمكن كتابتها في قانون وذلك من أجل تسهيل حفظها على كل مستخدميها فتكتب هكذا.
(الوتر)² = (الضلع الأول) ²+ (الضلع الثاني) ²
ويمكن أن تكتب هذه النظرية بالرموز وتكون هكذا أ² = ب² + ج².
ب، ج: أطوال أضلاع المثلث قائم الزاوية الأخرى.
أ: طول وتر المثلث قائم الزاوية.

خصائص المثلث قائم الزاوية

المثلث القائم الزاوية له الكثير من الخصائص المهمة ولكن يمكن تلخيص كل هذه الخصائص فيما يلي:

المثلث القائم الزاوية لا يمكن أن يصبح مثلث متساوي الأضلاع أبداً والسبب في ذلك أن طول الوتر في المثلث القائم الزاوية يكون دائماً أطول من باقي الأضلاع الأخرى داخل المثلث.
من الممكن أن يتحول المثلث القائم الزاوية إلى مثلث متساوي الساقين وذلك يحدث عندما يتساوى طول الضلعين اللذان يحصران بينهم الزاوية القائمة في المثلث القائم.
دائماً يكون طول المتوسط المرسوم من الزاوية القائمة في المثلث يساوي طول نصف القطر الموجود في المثلث.
المتوسط الذي يمتد من الوتر داخل المثلث القائم الزاوية يقسم المثلث إلى مثلثين متطابقين أو كما يقال ينصف المثلث ويكون ناتج هذا التصنيف هو ظهور مثلثين كل منهم متساوي الساقين.
المثلث القائم الزاوية والمثلث المختلف الأضلاع يحتوي كل مثلث منهما على زاوية واحدة قائمة وزاويتين حادتين يكون قياس كل منهما مختلف تماماً عن الأخر وأطوال أضلاع المثلثين تكون مختلفة أيضاً.
المثلث القائم الزاوية والمثلث المتساوي الساقين زاوية واحدة قائمة ويحتوي كل منهما على زاويتان حادتان يكون قياس كل زاوية منهما 45 درجة ويكون طول باقي الأضلاع الأخرى في المثلثان متساوية.

خصائص المثلث متساوي الساقين

المثلث المتساوي الساقين أو كما يطلق عليه في الإنجليزية Isosceles triangle وهو عبارة عن مثلث يمتلك ضلعان متساويان والضلع الآخر يكون مختلف.
قياس الزاويتان المقابلتان الأضلاع المتساوية تكون متساوية أيضاً في القياس ويطلق عليها زوايا الخاصة بالقاعدة.
في هذا المثلث تتساوى أطوال خطوط المتوسطات التي ترسم من الزوايا المتساوية في المثلث المتساوي الساقين.
الخط المتوسط في المثلث المتساوي الساقين يكون له نفس ارتفاع المثلث المتساوي الساقين.
الارتفاع الممتد من رأس المثلث المتساوي الساقين وحتى القاعدة ينصف القاعدة إلى قسمين متساويان وينصف أيضاً زاوية الرأس إلى قسمين متساويان.
القاعدة الموجودة في المثلث المتساوي الساقين تكون هي الضلع الثالث الذي لا يتساوى طوله مع طول أي ضلع من أضلاع المثلث.

خصائص المثلث مختلف الأضلاع

المثلث المختلف الأضلاع يعرف بأنه المثلث الذي يختلف جميع أطوال أضلاع تختلف جميع زواياه أيضاً ويطلق عليه في اللغة الإنجليزية Scalene triangle.
أطوال خطوط المتوسطات الثلاثة تكون مختلفة دائماً في المثلث المختلف الأضلاع.
لا يحتوي المثلث المختلف الأضلاع على نقطة تماثل.
لا يحتوي المثلث المختلف الأضلاع على خطوط تناظر.
لا يحتوي المثلث المختلف الأضلاع على أضلاع متساوية في الطول.
لا يحتوي المثلث المختلف الأضلاع على زوايا متساوية في القياس.
من الممكن أن تكون زوايا المثلث المختلف الأضلاع قائمة وأحياناً تكون هذه الزوايا منفرجة.

ملاحظات هامة لجميع أنواع المثلثات

من الممكن أن يمتلك المثلث الواحد اسمين فمن الممكن أن يكون المثلث القائم الزاوية في نفس الوقت هو مثلث متساوي الساقين وذلك بسبب أنه يمتلك ضلعين متساويين في القياس بالإضافة أنه لديه زاوية قائمة أيضاً.
المثلث القائم الزاوية يطلق على جميع أضلاع مسميات خاصة فالضلع المقابل للزاوية القائمة دائماً يسمي بالوتر أما بالنسبة لباقي الأضلاع يطلق عليهم الساقين.
يمكن استخدام نظرية فيثاغورس من أجل إيجاد أطوال أضلاع المثلث القائم الزاوية ويتم التعبير عن هذا القانون كالتالي.
(الوتر)²= (الضلع الأول) ²+ (الضلع الثاني) ².
الارتفاع في المثلث هو أحد الضلعين المتعامدين على الضلع الأخر أما في حالة اعتبار أحدهما هو الضلع الأخر العمودي عليه ففي هذه الحالة يعتبر قاعدة في هذا المثلث.

كيف يتم حساب مساحة المثلث؟

مساحة المثلث تعرف بأنها مقدار الفراغ الموجود داخل المثلث ويمكن حساب مساحة المثلث عن طريق مجموعة مختلفة من الطرق ومنها ما يلي:

1- حساب المساحة باستخدام أطوال الأضلاع

يمكن حساب مساحة أي مثلث باستخدام معلومية أطوال أضلاعه وتساوي نصف طول القاعدة الخاصة بالمثلث وتكون مضروبة في الارتفاع ويمكن كتابتها كما يلي مساحة المثلث = ½ × طول القاعدة × الارتفاع.
ويمكن كتابة هذا القانون عن طريق الرموز كما يلي.
م= ½ × ق × ع حيث أن ال ع هي ارتفاع المثلث وال ق هي طول قاعدة المثلث.

2- حساب مساحة المثلث باستخدام صيغة هيرون Heron’s formula

يتم استخدام صيغة هيرون في حساب مساحة المثلث بطريقة سهلة وبسيطة باستخدام القانون التالي:

مساحة المثلث=(س×(س-أ) ×(س-ب) ×(س-ج)) √ حيث أن.
ال ج هي طول الضلع الثالث من المثلث.
ال ب هي طول الضلع الثاني من المثلث.
ال أهو طول الضلع الأول من المثلث.

3- حساب مساحة المثلث بمعلومية طول الضلعين والزاوية المحصورة بينهما

يمكن حساب المساحة في هذه الحالة بطريقة سهلة جداً عن طريق القانون التالي.
مساحة المثلث= ½ × أ × ج × جا ب حيث أن ال أ هو طول قاعدة المثلث.
وال ج هي طول ضلع المثلث.
والزاوية ب هي الزاوية المحصورة بين الضلع الأول أ والضلع الثاني ج.