كل زاويتين متقابلتان في متوازي الأضلاع
كل زاويتين متقابلتان في متوازي الأضلاع ماذا يحدث لهما؟ يمكنك التعرف على الحل اليوم عبر موقع البلد ، حيث أنه من أهم القواعد التي يتم دراستها والتي تتعلق بمتوازي الأضلاع، بالإضافة إلى بعض الشروط الأخرى والتي تصنع الفرق بين الشكل المربع والمستطيل والمعين ومتوازي الأضلاع.
كل زاويتين متقابلتان في متوازي الأضلاع
من الخصائص التي نتعرف من خلالها على متوازي الأضلاع أن كل زاويتين متقابلتان في متوازي الأضلاع وكما نعرفه عنه بأنه من الأشكال المسطحة التي تكون ثنائية الأبعاد، ويتقابل كل ضلعين بشكل متساوي ومتوازي وسنقوم بتوضيح الخصائص الأخرى له في السطور التالية.
ما هو متوازي الأضلاع؟
يعد متوازي الأضلاع شكل هندسي يتواجد في الهندسة الإقليدية وهو شبيه بشكل المعين، ويعتبر شكل هندسي يحتوي على أربعة أضلاع متقابلين ومتوازيين، وداخله يكون الضلعان متساويين ومتوازيين في الطول، وكل زواياه متقابلة متساوية، وبه قطرين يقسمان بعضهما البعض ويكون مجموع الزوايا التي تتواجد به 360 درجة.
أهم خصائص متوازي الأضلاع
يمكننا التعرف على متوازي الأضلاع من خلال ملاحظة وجود الخصائص التالية:
- كل زاويتين متقابلتان في متوازي الأضلاع وهي الخاصية الأولى والأهم.
- تتكامل الزوايا التي يضمها متوازي الأضلاع وتقع كل زاويتين على ضلع واحد ويكون مجموعهما 180 درجة.
- في حالة وجود واحدة من الزوايا بشكل قائم تكون الزوايا المقابلة قوائم أيضًا وبالتالي يصبح الشكل مستطيلًا أو مربعًا وتعد حالات خاصة يظهر فيها متوازي الأضلاع بهذا الشكل.
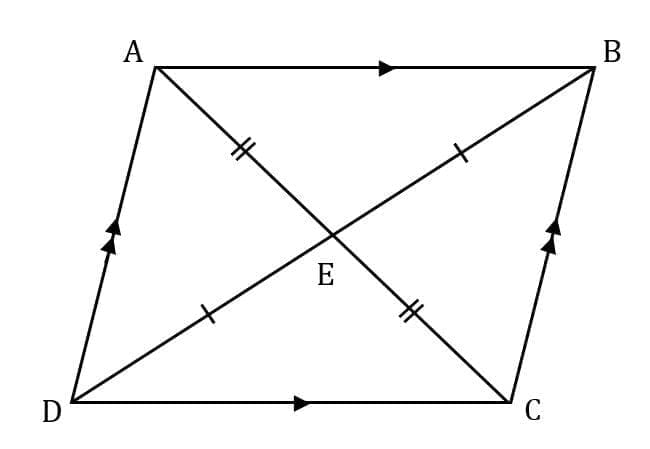
- يحتوي متوازي الأضلاع على قطرين، وتتواجد في شكل خطوط مستقيمة يتم رسمها بين الرؤوس التي يحتوي عليها متوازي الأضلاع والرؤوس التي تقابله، وللقطرين خصائص أولهما أن القطر الواحد يأتي في منتصف القطر الثاني، وعند وجود القطر يقسم المتوازي إلى مثلثين متطابقين.
- النقطة التي يلتقي فيها القطران تُسمى مركز التناظر وهي المركز الخاص بمتوازي الأضلاع.
- كل ضلعين في متوازي الأضلاع متقابلين متساويين.
- المساحة الخاصة بمتوازي الأضلاع تساوي ضعف المساحة الخاصة بالمثلث الذي يتمثل في ضلعين وقطر.
- في حالة مرور مستقيم في المركز الخاص بمتوازي الأضلاع يقوم بقسمه إلى شكلين متطابقين.
- يساوي مجموع المربعات الخاصة بالأطوال لمتوازي الأضلاع مربعي طول القطرين.
- مجموع الزوايا المتحالفة في متوازي الأضلاع 180 درجة.
الحالات الخاصة من متوازي الأضلاع
توجد بعض الحالات الخاصة بمتوازي الأضلاع وتتمثل في ثلاث أشكال هندسية وهم المعين والمستطيل والمربع وسنقوم بتوضيحهم في النقاط التالية:
- يعد المستطيل متوازي أضلاع وبه جميع الخصائص التي تُثبت ذلك ولكن توجد بعض الخصائص الأخرى التي تقوم بتميزه عن متوازي الأضلاع وتتمثل في أن زواياه بالكامل قائمة والأقطار الخاصة به متساوية طوليًا وتقسم زواياه.
- المعين شكل رباعي تتساوى أضلاعه في الطول، ويعد المعين متوازي أضلاع وبه جميع الخصائص التي تُثبت ذلك بالإضافة إلى بعض الخصائص الأخرى التي تقوم بتمييزه عن شكل متوازي الأضلاع، وتتلخص في كون أقطاره تكون متعامدة ويكون قياسها 90 درجة وبالتالي تنصف زواياه.
- المعروف عن المربع أنه متوازي أضلاع وبه الخصائص التي تُميز المستطيل والمعين، كما يتميز بوجود بعض الخصائص الأخرى بجانب التساوي في طول الأضلاع مثل المعين والزوايا القائمة وتساوي الأقطار مثل المستطيل، وتكون الأقطار متعامدة مثل المعين ومتطابقة مثل المستطيل وتنصف الزوايا.
محيط متوازي الأضلاع
يتم حساب محيط المتوازي الأضلاع عن طريق العلاقة التي يتم إيجادها حيث يكون a وb الطول للضلعين المتجاورين داخله وبذلك يكون قانون حسابه كالتالي:
طول الضلع الصغير + طول الضلع الكبير + طول الضلع الصغير + طول الضلع الكبير= المحيط
أو 2 (طول الضلع الكبير + طول الضلع الصغير)= المحيط
متى يكون الشكل الرباعي متوازي أضلاع؟
يصبح الشكل الرباعي متوازي أضلاع عند توافر الشروط التالية:
- في حالة وجود الأضلاع المتقابلة في الشكل الرباعي متطابقة.
- أن يكون الأضلاع المتقابلة متوازية.
- في حالة وجود ضلعين متقابلين ومتطابقين في الشكل الرباعي بالإضافة إلى كونهم متوازيين أيضًا.
- يكون كل قطر في الشكل الرباعي يأتي ينصف القطر الثاني.
- في حالة أن تكون الزاويتين متقابلتين في هذا الشكل الرباعي متساوية أيضًا.
- يكون مجموع الزوايا المتحالفة في ضلع واحد داخل الشكل الرباعي 180 درجة.
وبهذا نكون قد وضحنا مفهوم كل زاويتين متقابلتان في متوازي الأضلاع كما ذكرنا الخصائص التي يحتوي عليها متوازي الأضلاع وطريقة حساب محيطه والأشكال الهندسية التي تماثله في الخصائص.





