مساحة شبه المنحرف متساوي الساقين والقائم
مساحة شبه المنحرف متساوي الساقين والقائم هي ما تحتوي عليه السطور التالية عبر موقعنا البلد ويُطلق على شبه المنحرف في بعض الثقافات اسم آخر وهو رباعي الأطراف، والذي يحتوي على زوج واحد من الأضلاع المتوازية، كما سنتعرف في مقال اليوم على كيفية حساب مساحة شبه المنحرف وبعض الحقائق الهامة عنهما؛ فتابعونا.
ما المقصود بشبه المنحرف؟
قبل التحدث عن مساحة شبه المنحرف متساوي الساقين والقائم فإنه ُيقصد بشبه المنحرف الشكل الهندسي الذي يحتوي على أربع أضلاع متتالية يكون فيها زوج واحد منهم متوازيان.
يعتبر شبه المنحرف من الأشكال الهندسية الرباعية والذي يحتوي على ضلعين متوازيين في شبه المنحرف العادي أو ضلع قائم في شبه المنحرف القائم وتسمى هذه الأضلاع المتوازية قواعد.
كما تسمى زوج الزوايا التي تكون مشتركة في قاعدة شبه المنحرف بالزوايا الأساسية له، يمكن في شبه المنحرف أن يتساوى الضلعين غير المتوازيين في الطول، وفي هذه الحالة يسمى شبه منحرف متساوي الساقين ويكون في هذه الحالة الزوايا الأساسية متساوية في القياس.
قد تقع الجوانب المتوازية لشبه المنحرف في شكل رأسي أو مائل، ويطلق على المسافة العمودية بين الضلعين المتوازيين بالارتفاع الخاص بشبه المنحرف.
تتمثل قواعد شبه المنحرف في الجانبين المتوازيان مع بعضهما، كما يلاحظ تقاطع الأضلاع الأخرى في شبه منحرف إذا تم مدها فتشكل أرجل شبه المنحرف.
لمزيد من المعلومات عن طرق حساب مساحة شبه المنحرف
كيفية حساب محيط شبه المنحرف
قبل التعرف على كيفية حساب مساحة شبه المنحرف متساوي الساقين والقائم أتحدث في هذه الفقرة عن كيفية حساب محيط شبه المنحرف:
كما عرفنا من قبل أن الأضلاع المتوازية لشبه المنحرف تسمى القواعد، بينما الجوانب الأخرى لا تتوازى، ولكن امتداداتها تتقاطع مع بعضها في نقطة إذا تم مدها وتسمى بأرجل شبه المنحرف، ومن هنا يتم حساب محيط شبه المنحرف بالقانون التالي:
محيط شبه المنحرف= مجموع أطوال أضلاعه أو محيط شبه المنحرف= طول القاعدة الصغرى + مجموع الساقين+ طول القاعدة الكبرى.
مساحة شبه المنحرف متساوي الساقين والقائم
يكون الشكل الهندسي شبه منحرف إذا توفر به زوج فقط من الأضلاع المتقابلة المتوازية والمختلفة في الطول، أما في حالة شبه المنحرف الذي يحتوي على زاويتين قاعدة متساويتين يكون شبه منحرف متساوي الساقين.
ومن هنا يمكن حساب مساحة شبه المنحرف متساوي الساقين والقائم عن طريق القانون التالي:
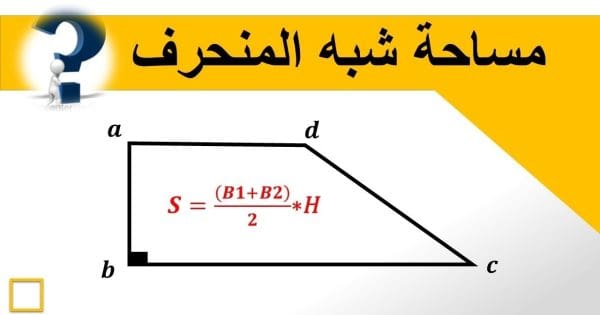
مساحة شبه المنحرف = نصف مجموع طول القاعدتين × الارتفاع.
أو بطريقة أخرى:
مساحة شبه المنحرف = نصف (طول القاعدة الكبرى + طول القاعدة الصغرى) × الارتفاع.
خصائص شبه المنحرف
- شبه المنحرف يعتبر شكل هندسي يحتوي على زوج من الأضلاع المتوازية المتقابلة.
- يملك شبه المنحرف متساوي الساقين أقطار متساوية في الطول لكنها لا تنصف بعضها البعض.
- يكون الجزء الأوسط لشبه المنحرف متكون من خط يربط بين النقاط الوسطى للضلعين غير المتوازيين، كما لا يوجد غير منصف واحد فقط في شبه المنحرف ويكون موازياً للقاعدة الكبرى والقاعدة الصغرى له.
أمثلة من الحياة على شبه المنحرف
لا يتواجد شكل مساحة شبه المنحرف متساوي الساقين والقائم في الحياة بشكل كبير بعكس الأشكال الهندسية الاخرى مثل المستطيل والمربع والدائرة، حيث نشاهد أشكالها في كل مكان من حولنا، لكن قد تتوفر بعض أشكال شبه المنحرف إذا قمت بالتدقيق في حقيبة يد أو أشكال الجسور أو صندوق الفشار.
معلومات حول شبه المنحرف
- يترجم كلمة شبه المنحرف في اليونانية القديمة إلى إسم معناه طاولة صغيرة، كما يعني الشكل رباعي الأجزاء غير المنتظمة.
- تم إدراج مصطلح شبه المنحرف في اللغة الإنجليزية عام 1570، وذلك على يد Marinus Proclus، الذي اعتبر أول من استخدم كلمة ومصطلح شبه المنحرف في كتاب العناصر.
- يطلق على أي شكل هندسي شبه منحرف عندما يكون شكل رباعي، خطوطه مستقيمة واثنان من أضلاعه متقابلان متوازيان.
- يتكون شبه المنحرف من جزئين الأول القواعد وهي الجانبان المتوازيان، والأرجل وهي الجانبان الآخران.
- عندما يتساوى الجانبين الغير متوازيان أو ما يعرف بالأرجل في الطول يكون شبه المنحرف متساوي الساقين.
- يمكن قياس محيط شبه المنحرف عن طريق جمع اطوال اضلاعه الاربعة، في حالة الجهل بقياس واحد أو أكثر من جوانب شبه المنحرف يمكن إنجازها لاستخدام نظرية فيثاغورس.
- إذا تم طلب إثبات أن شكل هندسي شبه منحرف، يمكن ذلك عن طريق إثبات أن ضلعين منه متوازيان والآخرين ليس كذلك.
أنواع شبه المنحرف
- شبه المنحرف مختلف الأضلاع: وهو يكون حالة من حالات شبه المنحرف حيث تكون أضلاعه الأربعة مختلفة في الطول، وتكون قاعدتيه متوازيتين ولكن ليس لهم نفس الطول، كما أن الضلعين الآخرين يكونان غير متوازيان وغير متساويان في الطول.
- شبه المنحرف متساوي الساقين: و هو حالة أخرى من شبه المنحرف، يكون فيه الساقين متساويين في الطول، أما قاعدتاه متوازيان ولكن ليس لهما نفس الطول.
- شبه المنحرف القائم الزاوية: وهو يملك زاوية قائمة واحدة أي 90° من زوايا القاعدة.
- شبه المنحرف حاد الزاوية: يحتوى هذا الشبه منحرف على زاوية حادة أي قياسها أصغر من 90 وتكون محصورة بين أحد ساقيه والقاعد الكبيرة.
إثبات أن شبه المنحرف هو شكل متساوي الساقين
يوجد العديد من الطرق التي يمكن اتباعها لإثبات أن الشكل شبه المنحرف متساوي الساقين نذكر منها:
- إذا كان شبه منحرف له زوايا قاعدة متساوية يكون متساوي الساقين
- يكون شبه المنحرف متساوي الساقين إذا كانت كل زاويتين متقابلتين متكاملتين.
شبه المنحرف القائم
ذكرنا من قبل حالة شبه المنحرف القائم الزاوية والذي يكون فيها أحد ساقي شبه المنحرف عمودية على القاعدة ويشكل معها زاوية قائمة 90 درجة ويمكن حساب مساحة شبه المنحرف متساوي الساقين والقائم بالاستناد إلى القانون العام لحساب مساحة شبه المنحرف والذي ينص على:
مساحة شبه المنحرف القائم= نصف ( مجموع أطوال القاعدتين الصغرى والكبرى) × طول الارتفاع.
ارتفاع شبه المنحرف
في العادة نحصل على ارتفاع شبه المنحرف بإسقاط عمود من أحد رؤوس القاعدة الصغرى على القاعدة الكبرى، ثم قياس طوله، ولكن في حالة شبه المنحرف القائم فإن الارتفاع يكون هو نفسه الضلع العمودي على القاعدة ويمكن حسابه كما أوجدنا مساحة شبه المنحرف متساوي الساقين والقائم كذلك.
مثال بسيط
يمكن توفير مثال بسيط للفهم كيفية الحصول على مساحة شبه المنحرف كما يلي:
أ ب ج د شبه منحرف فيه طول ضلعي القاعدة 10، 14 سم، بينما الارتفاع 5 سم، احسب مساحته.
الحل: بتطبيق قانون مساحة شبه المنحرف متساوي الساقين والقائم يكون:
المساحة= ((10+14)/2) × 5= 60 سنتيمتر مربع.
حساب طول الارتفاع من مساحة شبه المنحرف
يمكن نعكس القانون السابق لكي نحصل على الارتفاع اذا توفرت مساحة شبه المنحرف وطول القاعدتين وذلك عن طريق العلاقة التالية:
الارتفاع= المساحة ÷ نصف مجموع القاعدتين
مثال على إيجاد ارتفاع شبه المنحرف
لدينا شكل شبه منحرف قائم الزاوية تبلغ مساحته 252 سنتيمتر مربع، أما طول قاعدته الكبرى يبلغ 15 سم وطول قاعدته الصغرى 11 سم، أوجد طول ارتفاعه.
الحل:
في حالة شبه المنحرف هنا هو قائم الزاوية ويكون ارتفاعه هو ضلع الزاوية القائمة، ولحساب طوله نتبع العلاقة التالية:
الارتفاع = المساحة ÷ نصف مجموع القاعدتين.
الارتفاع = 252 ÷ ((15+ 11) ÷2) = 14 سم.
ونوفر لكم عبر الرابط التالي شبه المنحرف قائم الزاوية وأمثلة على حساب محيط شبه المنحرف القائم الزاوية
يعتبر مجال الهندسة من أكثر المجالات الرياضية التي تحتوي على نظريات كثيرة وأنواع متعددة فهو علم واسع يحتاج إلى فهم عميق وعقل ذكي؛ ولذلك عرضنا لكم اليوم مساحة شبه المنحرف متساوي الساقين والقائم بشكل مبسط وسلس، نرجو أن نكون قد أفدناكم وانتظروا المزيد من المواضيع الهادفة في الفترة القادمة.





