حل معادلة من الدرجة الثالثة
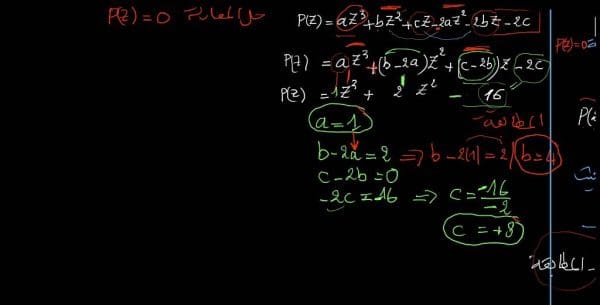
حل معادلة من الدرجة الثالثة أو ما تعرف بالمعادلة التكعيبية يتطلب إيجاد الجذر التكعيبي للدالة، وهو ليس بالأمر السهل، فهناك قانون عام يختص بحساب الجذور، وهو يعتمد على قيمة المعاملات، ويتم حل المعادلة عن طريق ثلاث خطوات كما هو موضح في السطور القادمة من خلال موقع البلد.
خطوات حل معادلة من الدرجة الثالثة
- حل معادلة من الدرجة الثالثة يتطلب أولا إعادة صياغة المعادلة لتكون على الصيغة المعيارية للمعادلات التكعيبية وهي (س3 + س2 + س + عدد= 0)، فلو كان لدينا معادلة على هذه الصيغة (س2 + 5س – 8= 14/س) فهي في الظاهر لا تبدو كمعادلة تكعيبية.
- ولكن عند ضرب الطرفين بالمتغير (س) فسوف نحصل على المعادلة التكعيبية (س3 + 5س2 + 8س= 4 ← س3 + 5س2 + 8س – 14=0)، وفي هذه الحالة يمكن القول بأننا حصلنا على المعادلة التطبيعية بصيغتها المعيارية.
- ولكي يتم حل هذه المعادلة فيجب أولا معرفة قيمة (س) التي تجعل المعادلة تساوي صفراً والتي تكون في هذه المعادلة تساوي واحد، بحيث إذا تم تعويض الرقم واحد مكان (س) في المعادلة فسوف تئول النتيجة إلى الصفر.
حل معادلة من الدرجة الثالثة
- بالاستناد إلى نظرية المعامل فإن (س=1) سوف يكون منها (س-1) هو معامل المعادلة السابقة (س3+5س2+8س-14=0) بحيث تصبح المعادلة على ذلك النحو← (س -1) ( س2 + س + عدد) حيث يوجد أعداد مرافقة للمتغيرات (س2، س) لابد من إيجاد قيمة كلٍ منهما مع قيمة العدد.
ولكي يمكن إيجاد قيمة هذه الأعداد يتم استخدام طريقة القسمة المطولة، حيث يتم أخذ قيمة المرافقات من المعادلة الأصلية، ثم يتم ترتيبهم في صف أفقي، ثم كتابة المعامل (س =1) ولكن يتم الفصل بينهم بخط عمودي، بحيث يضرب الناتج في الأسفل في قيمة (س)، ومن ثم يتم جمع الناتج مع قيم المتغيرات، كالتالي:
1 5 8 -14 | س = 1
_____________
1 6 14 |
1 6 14 0
- في النهاية حين نحصل على القيمة (صفر) بذلك يتأكد أن المعامل (س – 1) يمثل جذر المعادلة التكعيبية ” معادلة من الدرجة الثالثة “، ولكن إذا لم تساوي النتيجة الأخيرة صفر فذلك يعني أنه لا يوجد جذر لهذه المعادلة.
- ومن خلال النظر إلى أول ثلاثة أرقام بسطر الناتج نجد أنها تمثل معاملات المتغيرات للمعادلة التربيعية، والتي إذا ضُربت في المعامل (س -1) سوف نحصل على المعادلة التكعيبية الأصلية، وهي (س2 + 6س + 14)، ومنها تصبح المعادلة التكعيبية بهذا الشكل ← _س -1) (س2 + 6س +1).
الفرق بين حل معادلة من الدرجة الثالثة والصيغة
- قبل أن نجيب على هذا السؤال لابد أولا من معرفة أن كلا المفهومين واحد، ولكن الأصح هو أن كل صيغة معادلة ولكن ليست كل معادلة صيغة، فالمعادلة “Equation” تستخدم للتعبير عن شيئين متساويين ويتم الربط بينهما بإشارة المساواة، مثل: (5س+ 4 =0).
- ولكن الصيغة “Formula” تستخدم للتعبير عن قيمة ليست معروفة، فتأخذ شكل المعادلة لكي تضبط علاقة ما بين القيم المتغيرة، مثال على ذلك: ( قانون مساحة المستطيل = الطول X العرض ) وبذلك أخذت شكل المعادلة لكي تبين أن صيغة مساحة المستطيل تكون ثابتة من خلال ضرب الطول في العرض.
أشهر نظريات ورموز حل معادلة من الدرجة الثالثة في الرياضيات
هذه بعض من أشهر المفاهيم والرموز التي تستخدم في علم الرياضيات:
- الباي (π) وهي ترمز إلى المعدل بين محيط الدائرة يقسم على طول قطرها.
- المعادلة التفاضلية: وهي تساوي مشتقة (رقم أويلر e)، ويتم صياغتها على هذا النحو ←(f(x) = ex).
- نظرية فيثاغورس: وهي تنص على ← (أ) و (ب) الضلعان القصيران في المثلث القائم الزاوية، و (ج) هو الأطول في المثلث، وبالتالي فإن حسبا قاعدة المثلث يكون على هذا النحو ← (أ)2 + (ب)2 = (ج)2، بمعنى أن حاصل مجموع مربع أطوال الضلعين يساوي مربع طول الضلع الأكبر.
- النظرية الأساسية في علم حساب التفاضل والتكامل: وهي تعبر عن حقيقة أن كلا من عمليتي التفاضل والتكامل هما عكسيتان كل منهما للأخرى.
- النظام الخطي: وهذه المعادلة {ق (س) = عدد} تسمى بالمتجه، وتستخدم المعادلة لوصف العديد من الأنظمة الفيزيائية، وهي أيضا الحل الأمثل للمتغير (س).
حل معادلة من الدرجة الثالثة ذات العوامل الأولية
حل المعادلة يعتمد عل إذا كانت فرق بين مكعبين أو مجموع مكعبين، فيتم حلها على النحو التالي:
س³ – ص³ = ( س – ص) (س² + س ص + ص²)
س³ + ص³ = ( س + ص) (س² – س ص + ص²)
وفي هذه الحالة يكون
س³ – 4س² – 9 س – 36
= س² ( س + 4) – 9(س + 4)
= س² – 9 ( س + 4)
🙁 س – 3) (س + 3) (س + 4)
أما غير ذلك فيتم استخدام نظرية العوامل
المثال الأول
س³ + س² + س + 1 = 0
هكذا بالتقسيم نستطيع جعل المقدار على النحو التالي:
س³ + 1 + س² + س = 0
= (س+1) ( س² – س + 1 ) + س (س+1) = 0
بأخذ (س + 1 ) كعامل مشترك
إذن : (س+1) ( س² – س + 1 + س ) = 0
( س + 1 ) ( س² + 1 ) = 0
يلاحظ أنه لا يوجد تحليل لـ س² + 1 في حقل الأعداد الحقيقية .
المثال الثاني
س³ + 4س² + س – 6 = 0
بفرض أننا لا نعرف كيفية حل هذه المعادلة، فيمكن تجرب وضع ( س = 0) هل تتحقق المعادلة ؟
بالطبع لا فـوضع (س = )0 يعطينا (-6) لذلك لا تحقق المعادلة
إذن لنجرب وضع (س = 1)
(1)³ + 4(1)² + (1) – 6 = 0
بالفعل تتحقق المعادلة .. إذن (س – 1)
من أصفار المعادلة يتم القسمة عليه
س² + 5س + 6
ـــــــــــــــــــــــــــــــــــــــــــــ
س³ + 4س² + س – 6 | (س – 1)
س³ – س²
ـــــــــــــــــــــ بالطرح ـــــــــــــــــــ
5س² + س – 6
5س² – 5س
ـــــــــــ بالطرح ـــــــــــــــــــ
6س – 6
6س – 6
ـــــــــــــــ بالطرح ــــــــــــــــــ
00 00
إذن: (س – 1) (س² + 5س + 6)
وبذلك يتحقق تحليل المعادلة ، الآن فقط يتم تحليل ما داخل القوس ..
(س – 1) (س + 2) (س + 3)
ملاحظات عند حل معادلة من الدرجة الثالثة
عند حل المعادلات الجبرية فهناك بعض الأمور التي يجب مراعاتها، وهي:
الخطوة الأولى عند حل المعادلات الجبرية هي القيام بتجميع الحدود المتشابهة.
الحرص بشكلٍ دائم على طرح أو إضافة نفس القيمة لكلا الطرفين.
لكي يتم التخلص من الكسر فيتم ضرب الطرفين بمقلوب الكسر.
يجب الحرص على قسمة طرفي المعادلة باستخدام نفس العدد، ولكن بشرط ألا يساوي الصفر.
في بعض الحالات يمكن تطبيق بعض الاقترانات على طرفي المعادلة حتى يتم حلها، كما هو الحال في تربيع الطرفين.
تعرفنا معا على طريقة حل معادلة من الدرجة الثالثة باستخدام الصيغة المعيارية، وهناك العديد من المعادلات في علم الرياضيات، فعلوم الرياضيات بحر واسع من النظريات والرموز والمعادلات لا تنتهي دراساته وتطبيقاته.





